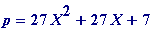The Jacobi order 9 primes: two other quadratics

From: [email protected]
To: Andrew Granville (E-mail)
Cc: [email protected]
Subject: 3m^2+3m+1
Sent: Fri, 17 Dec 2004 15:42:34 +0000

Dear Andrew, You have Maple, don't you? Here, at home, I've got Maple 6. I'm taking the liberty of sending you a small Maple worksheet I started this morning, and which I've just completed. I've removed all output to reduce its size. I hope it's free of errors, and that you will find it of interest. I've never tried to attach a file from here through the university remote site, so I'm just hoping this works. Take care, John

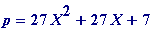fell into my lap on the evening of Wed 15th December 2004

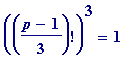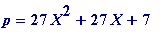The following conjecture appears to be true (its proof is the real problem). (mod p ) for prime p = 1 (mod 3) if and only if for some integer X . It (the above polynomial) came about from considering 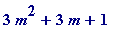with m restricted to m = 3 X + 1. Andrew saw it too - via a different route - at the same time!

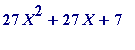forced the resulting primes to have a single '3' in the prime factorisation of ( ). At the time I thought - such an ugly polynomial, but with such a beautiful consequence. In this worksheet I simply want to emphasise the centrality of the original polynomial 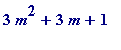(I believe an eventual proof of the above conjecture will come from somehow exploiting the fact that consecutive cubes mod p are solutions of the congruence 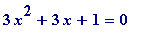(mod p ); I've put in a lot of work on that, although with no success so far...)

Weeks ago - while seeking examples of primes p (having what I would like to call the -structure):

, with primes ( ) subject to or ,

hoping that all generated primes would satisfy 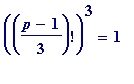(mod p ), I did the following type of calculation:

> P[1,3] := proc(p) local r, k; r := 1;
for k from 2 to (p-1)/3 do
r := mods(r*k, p) od; r; end:

>

In the following I should have started the 'k' at 3, to push up the least value of (= ithprime(k)) to 5, but, with hindsight, I'm happy to have done a foolish thing, because without it I would probably not have stumbled upon a new insight , the correct way to view 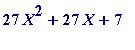(explained in its proper place below).

> alpha := 1: for k to 100 do
# q[1] being ithprime(k)
if isprime(2^alpha*ithprime(k)+1)
and isprime(2^alpha*3*ithprime(k)*(2^alpha*ithprime(k)+1)+1)
then print(2^alpha*3*ithprime(k)*(2^alpha*ithprime(k)+1)+1,
P[1,3](2^alpha*3*ithprime(k)*(2^alpha*ithprime(k)+1)+1)^3
mod (2^alpha*3*ithprime(k)*(2^alpha*ithprime(k)+1)+1)) fi od;

>

Seeing that (127, 19) output - three weeks ago today - gave me a terrible shock (even with those four 1's), until I realised what was going on: with 'k' - by default - starting at '1', the that was producing that offending '127' was an extra '3' in the prime factorisation of ( ): 127 - 1 = (2^1)*[3]*3[an extra 3]*7. Relief all round...

But, did the '19' in (127, 19) correspond to anything? Of course it did:

> 19^3 mod 127;

>

Thus, while neithe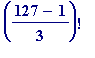r nor 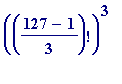came to be 1 (mo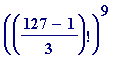d 127), did come out to be 1 mod 127.

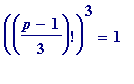The obvious thought - at the time a distraction (one of simply too many others all coming in at the same time), but to revisit at some future date - was that if one modified the alpha-structure for prime p to allow to be 3 then, if p doesn't have the beautiful property that (mod p ), perhaps it has the (still quite lovely) property that 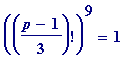(mod p ) as a compensation. In short, these primes p could be of interest:

, with prime or

Here, now, are some of them. I don't allow to get beyond 6 where a computation is concerned, because that takes a serious amount of time to compute.

> # here p = 2^alpha*9*(2^alpha*3+1)+1
for alpha to 50 do
if isprime(2^alpha*9*(2^alpha*3+1)+1)
then print(alpha, 2^alpha*9*(2^alpha*3+1)+1) fi od;

> # here p = 2^alpha*9*(2^alpha*3-1)+1
for alpha to 50 do
if isprime(2^alpha*9*(2^alpha*3-1)+1)
then print(alpha, 2^alpha*9*(2^alpha*3-1)+1) fi od;

>

Now to compute those orders, to see they all pick up an extra '3'

> with(numtheory): # for use of order command

Warning, the protected name order has been redefined and unprotected

> # here p = 2^alpha*9*(2^alpha*3+1)+1
for alpha to 8 do
if isprime(2^alpha*9*(2^alpha*3+1)+1)
then print(alpha, 2^alpha*9*(2^alpha*3+1)+1,
order(P[1,3](2^alpha*9*(2^alpha*3+1)+1), 2^alpha*9*(2^alpha*3+1)+1)) fi od;

>

> # here p = 2^alpha*9*(2^alpha*3-1)+1
for alpha to 8 do
if isprime(2^alpha*9*(2^alpha*3-1)+1)
then print(alpha, 2^alpha*9*(2^alpha*3-1)+1,
order(P[1,3](2^alpha*9*(2^alpha*3-1)+1), 2^alpha*9*(2^alpha*3-1)+1)) fi od;

>

Now to come to the point:

the essential polynomial is 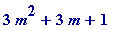in general ,
rather than 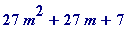in particular

Of course the primes we're really interested in happen to be those of the form 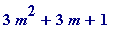, where we restrict m to the arithmetic progression (3 M +1), but look at the lovely things that happen when we allow m to run through the other two related progressions, 3 M and 3 M +2:

First, our old friends, the beautiful primes:

> for m from 1 by 3 while 3*m^2+3*m+1 < 10^5 do
if isprime(3*m^2+3*m+1)
then print(3*m^2+3*m+1, ifactor(3*m^2+3*m),
order(P[1,3](3*m^2+3*m+1), 3*m^2+3*m+1))
fi;
od;

Here m = 3 M . ( )'s prime factorisation has to pick up at least one extra 3, and in certain cases some others, but always the order seems to be fixed at 9:

> for m from 3 by 3 while 3*m^2+3*m+1 < 10^5 do
if isprime(3*m^2+3*m+1)
then print(3*m^2+3*m+1, ifactor(3*m^2+3*m),
order(P[1,3](3*m^2+3*m+1), 3*m^2+3*m+1))
fi;
od;

Here m = 3 M +2. Again, ( )'s prime factorisation has to pick up at least one extra 3, and in certain cases some others, but always the order seems to be fixed at 9:

> for m from 2 by 3 while 3*m^2+3*m+1 < 10^5 do
if isprime(3*m^2+3*m+1)
then print(3*m^2+3*m+1, ifactor(3*m^2+3*m),
order(P[1,3](3*m^2+3*m+1), 3*m^2+3*m+1))
fi;
od;

>

In fact the following appears to be true : 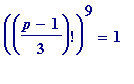(mod p ) (but not 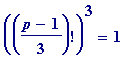(mod p )) for prime p = 1 (mod 3) if and only if 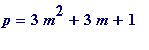for some integer (mod 3). (i.e., ). Not quite as beautiful a result as the original, but it does appear to be more deterministic:

rigid '9', rather than 1 or 3.